Mathematic Routes: Learning Experiences Beyond the Classroom
Paola Alejandra Balda Álvarez
This is an abbreviated version of the article.
Mathematics is everywhere. With mathematics, we can read, interpret, and transform society.
Mathematics is part of our daily lives; it is on the streets, in the shops, in cooking recipes, in our dance, in construction, in nature, in the ways we communicate with each other.
In this article, I share some guidelines based on a methodological idea that aims to show the presence and importance of mathematics in extracurricular contexts, through a learning model presenting situations that allow students to pass through three stages.
Model for learning experiences
The learning experience starts from a particular strategy: a real mathematical route, which is a tour of the locality, showing the presence of mathematics in the daily lives of the people who live in the area, as well as the mathematical forms or structures that configure a determined scenario.
The examples outlined in this article are part of classroom experience conducted with tenth- grade students in Colombia. General topics of Trigonometry and Analytical Geometry were
used in the lessons; however, these experiences apply for any subject, adjusted by the teacher after reflection.
Learning proposal: mathematical journeys as tourists
The learning experience of this project was structured through abductive reasoning. It was conceived as a series of mathematical tours through the locality in which the students live and study.
This learning experience used questions to guide students through three phases:
-
the exploratory phase, where students investigated and conjectured about the mathematical aspects identified in their specific environment;
-
the procedural phase, in which they checked the results of their explorations and conjectures with consolidated mathematical activities; and
-
the consolidation phase, that guided students to establish relationships and make generalizations or abstractions from the information they had obtained in the exploratory and procedural stages.
During the development of the proposal, the students made use of resources they constructed in the classroom for expensive measurements (clinometers), calculators to perform calculations, cell phones to photograph places and record videos, and parts of their body to calculate measures. The mathematical aspects that were considered in the learning experience were:
Learning experience applied to mathematics
-
Geometric shapes
-
Reference systems and the straight line
-
The circumference, the ellipse, and the parabola
-
Relationships and variations
-
Inaccessible measures and proportionality
Below are considerations and examples from the project of how the learning experience was organized, including the onsite work and the procedural and consolidated parts.
Geometric shapes
As Corbalán mentions (2007, p.3), “in school, there is a preponderance of planes, but in our environment, everything is three-dimensional.” So, this richness has permitted us to generate specific questions about the various shapes found in a given place, questions that
go beyond identification, and lead to an exploration of characteristics, reflections about their reason for being, and the consolidation of their properties definitions (Figure 1).

Figure 1. Work using geometric figures done by one of the students (Balda, 2019). Exploratory phase for geometric shapes
Many of the things around us have specific shape: floors, walls, stained glass, doors, and windows.
-
What shapes do you see in the place you visit? Take a photo and then draw its geometric representation.
-
Why do you believe these places or objects should have these shapes and not others? For example, would it make sense for a door to be round?
-
If you could change some shape, which one would you change and why?
-
Find someone who lives nearby and knows the history of the local church and ask him or her the following questions. Take photos of them and ask for permission to post them. Transcribe the answers that they give.
-
Who built the church?
-
What kind of art is observed in its construction? Procedural phase for geometric shapes
-
About the geometric shapes you found in the place:
-
Do you know the measurements of the figures you identified in the church? Estimate them, then check them by making real ones. Draw them to scale in your notebook. What instruments did you use to take the measurements?
-
What properties do you see in each of the figures? How would you describe them to someone who has never seen them?
-
Research the names of the geometric figures you found at the site. Investigate what are the properties of those geometric shapes and check those against the real ones.
-
Consolidation phase for the geometric shapes
-
In the procedural phase, you drew the figures in a reference system and deduced some properties. With those properties, how would you define those shapes?
-
In the church, you saw: Lines? Circumferences? Parabolas? Ellipses? Hyperbolas? Why do you think they have these shapes? How would you find their equations?
-
Needs a reference system and a straight line.
-
This highlights some ways of determining locations, methods of building, or making use of conventional reference systems (cartesian planes) to locate places precisely, determining distances, and finding places located at midpoints.
- The circumference, the ellipse, and the parabola
Usually, in textbooks, geometric figures are worked from the algebraic part, not knowing their properties and applications in real life. This exercise of recognizing where these shapes are located, their properties, and why particular objects in the environment have this form par excellence and no other, leads to a first approach to the objects in question, where the properties are inferred in light of their observable characteristics. This exercise seeks not only to identify geometric places as objects in the environment (Figure 2) but also that students feel the need to represent them through algebraic expressions for their exploration and as a tool for manipulating the object and studying its variations.

Figure 2. Work on a circumference elaborated by one of the students (Balda, 2019).
As noted below, the exploratory and procedural phase coincides with the one presented in the stages of geometric figures:
Exploratory phase for the circumference, the ellipse, and the parabola
Many of the things around us have particular forms.
-
What shapes do you see in the place you visit? Take a photo, and then make its geometric representation.
-
Why do you think those places or objects should have those shapes and no others?
-
If you could change some shape, which one would you change and why? Procedural phase for the circumference, the ellipse, and the parabola
-
Regarding the geometric shapes you found in the place:
-
Do you know the measurements of the shapes you identified? Estimate them, then check them through real measurements. Draw the shapes to scale in your notebook. What instruments did you use to measure them?
-
What properties do you see in each of the shapes? How would you describe them to someone who has never seen that figure?
-
Research the names of the geometric shapes you found at the site. Investigate what properties the figures have and check them against the real ones.
-
Draw the figures in a reference system and deduce the geometric properties of each one. What are you observing? What do you conclude?
-
Consolidation phase for the circumference, the ellipse, and the parabola
-
How would you algebraically represent the properties of the shapes? Relationships and variations
Relationships are correspondences between elements in two sets, which allow identifying how a determined mathematical entity can be expressed as mathematical functions of other entities. The exercise carried out within the framework of this learning experience aims to train students to be able to establish the dependent relationships among the ingredients in a recipe by performing an in-depth analysis that allows them to characterize dependencies of various types (Figure 3).
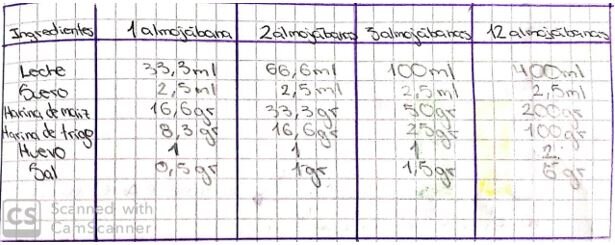
Figure 3. Work on dependent relationships elaborated by one of the students (Balda, 2019). Exploratory phase in relationships and variations
-
Find the recipes for making almojábana (cheesecake) and garulla (cheese bread) [1]. Procedural phase
-
List the ingredients used to make almojábana, then the listing of ingredient quantities for two, three, and a dozen.
-
Make a graphical representation of the relationships between the ingredients. How does the model look like? Describe it. What is the purpose of having a graphic model of those relationships?
-
Find out the cost of one almojábana and one garulla. Then go to the store and find out the price of the ingredients to make them. How much does each product earn? What percentage does the profit represent?
-
Consolidation phase in relationships and variations
-
Look for an algebraic model that represents the relationships among the product ingredients.
-
Look for a graphical model that represents the relationships among the product ingredients.
-
Why are the models useful? Which model do you find best for making predictions or generalizations? Why?
-
Let’s take math out of the classrooms and into everyday life
-
Observing the role that mathematics plays in social life is a long process that requires learning. Like almost everything in education, to be effective, it is necessary to be done many times to become a daily task.
-
Questions were asked at each stage of the learning experiences that guided the work. With the launch of this experience, other issues arose that made the discussions more interesting and directed.
-
I invite teachers interested in the subject to replicate this proposal that I share in the article, adapting it to their contexts and interest in learning in a way that becomes a representative experience for the student. It would be handy if you apply this methodology and share the results. I would like to hear from you. You can write to my e-mail.
About the author
Paola Balda teaches mathematics at the General Santander Educational Institution in Colombia. She has her Bachelor of Mathematics, Masters in Teaching Mathematics, and Doctor of Education. Her line of research is the social construction of mathematical knowledge.
References
-
Corbalán, F. (2007): “Rutas matemáticas por nuestra localidad”. Sigma, no 30, 105-116.
-
Balda (2019). Rutas matemáticas por el municipio de Soacha. Revista UNO. N83 (octubre 2019)
-
Balda (2018). Una epistemología de usos de lo proporcional. Un estudio socioepistemológico en el contexto de la huerta escolar. Tesis doctoral no publicada. Universidad Santo Tomás. Bogotá-Colombia.
-
Cantoral, R. (2013). Teoría Socioepistemológica de la Matemática Educativa. Estudios sobre construcción social del conocimiento. Barcelona: Gedisa.
-
MEN (2006). Estándares Básicos de Competencias. Ministerio de Educación Nacional. Bogotá-Colombia.
-
Novo M., Serrano, A. Alsina, Á. (2016). Educación matemática realista en educación infantil: “redescubriendo el teatro Calderón de Valladolid”. En Berciano, Ainhoa; Fernández, Catalina; Fernández, Teresa; González, José Luis; Hernández, Pedro; Jiménez, Antonio; Macías, Juan Antonio; Ruiz, Francisco José; Sánchez, María Teresa (Eds.), Investigación en Educación Matemática XX (p. 629). Malaga, España: Universidad de Málaga.
-
Reyes Gasperini, D. (2015). Empoderamiento docente desde una visión socioepistemológica: una alternativa para la transformación y la mejora educativa. (Tesis de doctorado). Centro de investigación y Estudios avanzados del Instituto Politécnico Nacional, Ciudad de México, México.
-
Paola Alejandra Balda Álvarez
https://observatory.tec.mx/edu-bits-2/mathematics-routes-learning-experiences-beyond-the-classroom